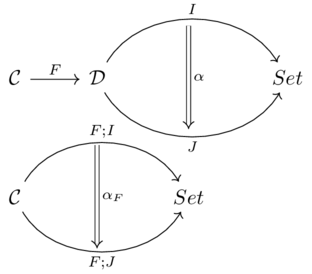
The pullback of functor \(\mathcal{D}\xrightarrow{I}\mathbf{Set}\) along functor \(\mathcal{C}\xrightarrow{F}\mathcal{D}\)
The composite functor \(\mathcal{C}\xrightarrow{F;I}\mathbf{Set}\)
Given a natural transformation \(I \overset{\alpha}\Rightarrow J\), there is a natural transformation \(\alpha_F\) whose components (morphisms in Set from \((F;I)(c)\) to \((F;J)(c)\), for any \(c \in \mathcal{C}\) are given by: \((\alpha_F)_c := \alpha_{F(c)}\)
Pulling back data along a functor
We’ll migrate data between the graph-indexing schema Gr and the loop schema, called DDS (for discrete-dynamical system).
We’ll write down an example instance \(\mathbf{DDS}\xrightarrow{I}\mathbf{Set}\)
| State | Next |
|---|---|
| 1 | 4 |
| 2 | 4 |
| 3 | 5 |
| 4 | 5 |
| 5 | 5 |
| 6 | 7 |
| 7 | 6 |
We want to convert this state information into a graph that will let us visualize our machine.
Use the following functor \(F\):
src is sent to identity
Can now generate a graph using the composite functor \(\mathbf{Gr}\xrightarrow{F}\mathbf{DDS}\xrightarrow{I}\mathbf{Set}\)
| Arr | src | tar |
|---|---|---|
| 1 | 1 | 4 |
| 2 | 2 | 4 |
| 3 | 3 | 5 |
| 4 | 4 | 5 |
| 5 | 5 | 5 |
| 6 | 6 | 7 |
| 7 | 7 | 6 |
\(Vert = \bar{7}\)
We can now draw the graph:
This procecure can be called “pulling back data along a functor". We pulled back data \(I\) along functor \(F\) (via functor composition).
Consider the functor \(\mathbf{Gr}\xrightarrow{G}\mathbf{DDS}\) given by sending src to next and tar to id on State. Migrate the same data as in Example 3.65 and draw the corresponding graph.NOCARD
| Arr | src | tar |
|---|---|---|
| 1 | 4 | 1 |
| 2 | 4 | 2 |
| 3 | 5 | 3 |
| 4 | 5 | 4 |
| 5 | 5 | 5 |
| 6 | 7 | 6 |
| 7 | 6 | 7 |
